- 세린
- 조회 수 4415
- 댓글 수 4
- 추천 수 0
쌍둥이는 합동일까? 닮음일까?
중학교 2학년 학생들은 2학기 중 70퍼센트 이상 도형에 대해 배운다. 정의, 정리, 증명에 대한 개념을 배우고, 실제로 삼각형이 가지고 있는 성질들과 여러 가지 사각형의 성질과 조건들을 증명한다. 그리고 도형의 닮음을 배운다. 오늘은 도형의 닮음에 대해서 이야기 해보자.
난 도형의 닮음을 배우는 시간이면 늘 학생들에게 먼저 누굴 닮았냐고 물어본다.
“혜리는 누구 닮았어?”
“아빠요.”
“재현이는 누구 닮았어?”
“음…… 엄마 반, 아빠 반?”
“그럼, 정수는?”
“전 할머니 닮았다는데요?”
많은 학생들에게 돌아가면서 질문을 하다보면 별별 대답이 다 나온다. 얼굴 윗부분은 엄마고, 아랫부분은 아빠라는 학생들도 있고, 누구도 안 닮았다고 하는 애들도 있고, 닮고 싶지 않다고 닮음을 거부하는 학생들도 있다.
“그럼 도형이 닮았다는 건 뭘까?”
정답을 아는 친구들이 있다. 선행학습의 결과다. 하지만 모르는 친구들도 많다. 도대체 도형이 닮은게 무엇인지, 내가 엄마, 아빠를 닮은 것과 무슨 관계가 있는지 궁금해 하는 친구들이 있다. 다행이다. 나는 그림을 그리기 시작 한다.
“자 봐봐!”
휴대폰 속 사진을 연상시키는 간단한 그림이다. 네모난 프레임에 여학생 하나를 그린다. 그리고 사각형 가로와 세로에 화살표를 그린다. 우리가 휴대폰으로 사진을 찍고 편집을 하려는 상태를 보여주는 것이다.
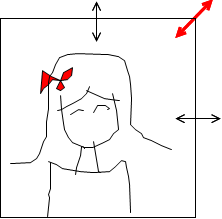
“애들아, 너희들 휴대폰으로 사진 많이 찍지? 그리고 너희들 홈페이지에 얼굴 올리잖아. 거짓말처럼 예쁜 사진들? 그치? 근데 그때 사진을 올리려는데 홈페이지 프로필 사진의 프레임에 잘 맞지 않는 경우가 있어. 즉 사진을 잘라야 할 때가 생기지. 잘못하면 얼굴이 반쯤 짤려서 올라가잖아. 그럼 우리는 어떻게 하지? 사진을 편집하지. 그때 가로만 줄이게 되면 얼굴이 가로로 길게 늘어나면서 뚱뚱하게 찌그러지지? 또는 세로로 줄이면 얼굴이 홀쭉해지면서 스크림 얼굴되잖아.”
아이들이 웃는다. 아마 내 표정이 우스꽝스러워서 일꺼다. 집중하게 하려면 표정이 다양해야 한다. 웃음이 좀 그치면 나는 다시 설명한다. 그렇게 얼굴을 이상하게 찌그러트리지 않고, 다만 사이즈만 조금 줄이려면 어떻게 해야할까? 우리는 가로와 세로에 있는 화살표가 아니라 한 꼭지점에 숨어 있는 화살표를 찾아 대각선 방향으로 일정하게 사진을 줄여야 할꺼다. 그럼 아이들이 고개를 끄덕인다.
이렇게 사진을 줄이거나 늘리는 것처럼 한 도형을 일정한 비율로 확대하거나 축소한 것이 다른 도형과 합동이 될 때, 이 두 도형은 서로 닮은인 관계에 있다고 한다.
“엄마나 아빠랑 내가 닮는 것이랑 도형이 닮았다는 것이 같은 말일까?”
아이들은 일제히 아니라고 이야기 한다. 맞다. 도형끼리 닮았다고 이야기 하는 것과 인간과 인간이 닮았다고 하는 것은 다른 이야기다. 수학에서 이야기 하는 ‘닮음’의 뜻이 따로 있다는 것을 인식시켜주고 싶다. 일상어와 착각하기 쉬운 수학 용어 때문에 오류를 범하는 경우가 많기 때문이다. 그때 수진이가 질문을 한다.
“선생님 쌍둥이는 합동이에요, 닮음이에요?”
아이들이 서로 대답한다. 몇몇은 합동이라고, 몇몇은 닮음이란다. 쌍둥이인 은진이는 아무것도 아니란다. 유진이는 유진이고 나는 나라면서 이란성이라고 주장한다.
“합동인거 같은데?”
내가 말했다. 아이들이 웃는다. 은진이는 골이 났다. 내가 왜 걔랑 합동이냐면서 말이다. 아이들을 진정시키고 다시 이야기한다. 쌍둥이가 서로 많이 닮았을 때 합동이라고 이야기 하는 것은 기막힌 표현방법이라고 말이다.
수업은 계속 된다. 다시 질문한다.
“도형의 닮음을 제일 먼저 발견한 사람이 누구일까?”
책에 보면 유클리드와 르장드르가 나와 있다. 아이들이 유클리드요, 르장드르요, 한다. 내가 아니라는 눈짓을 보내니 애들이 아리스토텔레스, 아르키메데스, 데카르트라면서 난리다. 자기가 아는 수학자는 다 나오는 것 같다. 어디선가 조용히 한 친구가 말한다.
“탈레스?”
“오! 누구야?”
“저요, 저요!”
지원이는 작은 소리로 내 밷었다가 맞았다는 말에 자신감을 얻었는제 손을 들고 표시한다. 자기가 탈레스라고 이야기 했다면서 소란이다.
“오, 지원이가 이야기했구나. 맞아. 탈레스가 제일 처음 발견한 사람이야. 탈레스는 소크라테스보다 이전 사람이거든....... 너희들이 이야기 한 다른 수학자 또는 철학자들은 다 탈레스보다 나중 사람이지.” 하면서 나는 탈레스 이야기를 약간 패러디 해서 들려준다.
탈레스가 친구와 함께 이집트를 여행하던 중이었다. 열아홉살 이집트 소년은 그들을 피라미드 앞으로 안내했다. 그리고 피라미드가 자신의 나라 이집트의 수학과 과학이 얼마나 대단한지 아주 잘 보여주는 건축물이라고 자랑했다. 탈레스와 친구는 피라미드의 웅장함 앞에서 입이 떡 벌어졌다. 특히 소년이 설명해 준 쿠프 왕(B.C. 2580년경)의 피라미드는 눈앞에 보이는 3개의 피라미드 중 가장 큰 피라미드였다. 그 순간 탈레스는 궁금증이 생겼다. 소년에게 물었다.
“근데, 저 쿠프 왕의 피라미드의 높이는 얼마인고?”
열아홉살 소년은 눈이 휘둥그레졌다. 이제까지 그런 걸 물어보는 사람은 한명도 없었기 때문이다.
“그게……, 저……”
당황한 소년은 우물쭈물 하다가 그 마을 어른에게 여쭤보고 오겠다고 하면서, 아마도 아는 사람이 없을거라고 하고 뛰어갔다. 탈레스는 소년에게 답을 얻을 수 없겠다고 생각하고 쿠프 왕의 피라미드 높이를 잴 방법을 궁리했다. 시간이 얼마나 지났을까, 탈레스는 쿠프 왕의 피라미드 높이를 알아냈다. 딱 세가지 요소를 가지고 말이다. 태양이 높이 솟은 그 시각 탈레스는 자신의 그림자를 보고 의미심장한 미소를 지을 수 있었다. 자신의 키와 자신의 그림자 길이 그리고 쿠프 왕 피라미드의 그림자 길이를 그는 세 요소로 가지고 왔다. 그리고 비례를 생각했다.
“내 키대 내 그림자 길이는 피라미드 높이 대 피라미드 그림자 길이지. 이때 모르는 것은 피라미드 높이 하나이니 우린 비례를 이용해 피라미드의 높이를 구할 수 있다네.”
소년이 뛰어왔다. 소년은 어떤 답도 가지고 오지 못했다. 그리고 탈레스의 설명을 듣고 쿠프 왕 피라미드의 높이를 알았다. 아마 모르긴 몰라도 그 소년은 탈레스와 친구가 돌아간 뒤 오는 여행객들에게는 자랑삼아 높이도 알려줬을 것이다.
이 이야기에서 등장한 식이 하나 있다. 그것을 바로
(탈레스의 키) : (탈레스의 그림자 길이) = (피라미드 높이) : (피라미드의 그림자의 길이) 이다.
탈레스가 발견한 닮음 도형의 성질이다. 삼각형의 닮음을 이용하여 이집트의 피라미드 높이를 구한 것이다. 우린 그것을 일목요연하게 정리해 21세기 수학 시간이 배우고 있는 거다. 학생들에게 이것을 다시 한 번 이야기 해준다. 우리가 배우는 수학은 아주 옛날에 발견한 것들이다. 그들의 지혜로 우리는 건물을 설계할 수 있다. 아주 정밀하게 설계하고 원하는 건물을 지을 수 있다. 지금 우리가 앉아 있는 이 곳도 처음에는 설계도면을 통해 그림이 그려졌을 것이다. 그리고 그것이 이렇게 실물로 나타나 우리가 사용할 수 있게 된 것이다. 도형의 닮음이 사용된 예 중 우리 실생활을 편리하게 해주는 것이 바로 지도다. 요즘 스마트 폰을 많이 사용하고 있어서 길찾기가 손쉬워졌는데, 우리가 보는 지도들도 다 도형의 닮음을 이용했다. 실제거리는 일정한 비율로 줄여 우리 손 안에 들어오게 한 것이다. 우리는 그 작은 지도를 보고 내가 가야할 장소를 찾아갈 수 있다. 특히 건축학과에 가고 싶은 친구들은 비례식, 도형의 닮음에 대한 감각이 탁월 할수록 유리할 것 같다.
어떤 도형을 확대하거나 축소했을 때 똑같아지면 즉, 합동이 되면 우리는 두 도형이 서로 닮았다고 한다. 그리고 닮은 두 도형의 대응하는 변끼리 길이의 비를 잘 따져보면 하나의 비율이 나온다. 그것을 닮음비라고 한다. 이 세상에서 늘 닮은 도형들이 몇 개 있는데 한 번 생각해보자. 어떤 도형이 늘 닮았을까? 정씨와, 원이다. 정씨는 뭐냐면 정삼각형, 정오각형, 정육각형 …… ‘정’이라는 단어가 붙은 도형들이다. 즉 모든 변의 길이가 같은 도형들은 다 닮았다. 같은 비율로 늘어나고 줄어들기 때문이다. 그리고 원도 늘 닮았다. 원은 원의 중심으로부터 반지름만 늘어나기 때문이다. 더 있다. 어떤 도형이 늘 닮았을까? 이것은 퀴즈다. 답은 밑에 공개하도록 하겠다. 도형들 중에는 늘 닮음인 애들이 있고, 따져보고 재봐야 닮음인 애들이 있다.
오늘 만큼은 주변 사물들을 볼 때 도형의 닮음의 관점으로 보는 것은 어떨까? 닮은 도형의 특징들을 저절로 파악할 수 있게 될 것 같다. 또 일상생활에서 이야기 하는 닮음에 대해서도 생각해 보며 엄마, 아빠 얼굴 한 번 더 보고 서로 어디가 닮았는지 이야기 해보자. 이야깃거리가 풍성해 질 것 같다. 다음 시간에는 도형 중에서도 특별한 삼각형의 닮음 이야기를 들어보도록 하자!
<참고 : 탈레스 이야기에 등장하는 쿠프 왕 피라미드는 실제로 가장 큰 피라미드이긴 하지만 탈레스가 그 피라미드의 높이를 쟀다는 사실은 밝혀지지 않았습니다. 이야기를 재구성했음을 알려드립니다.>
퀴즈 정답은? 직각 이등변 삼각형! (평면도형) / 구 (입체도형), 입체도형에서도 정씨! 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체 등
| 번호 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|
| 3252 | 눈 내린 풍광을 두고 울고 싶어라 -샤프란블루 [1] |  | 2012.11.19 | 6455 |
| 3251 | 쌀과자#29_사람을 알아보는 눈 [1] | 서연 | 2012.11.19 | 5517 |
| 3250 | 꿈쟁이 뿌꼬 #2 [4] | 한젤리타 | 2012.11.19 | 7134 |
| 3249 | 알려지지 않은 신 2 [2] | 레몬 | 2012.11.18 | 2869 |
| 3248 | 박지원을 통해 본 여행의 기술 |  | 2012.11.13 | 2869 |
| 3247 | 나이 50대, 아직도 영웅의 꿈이 지속 되는가? [1] | 학이시습 | 2012.11.13 | 3085 |
| 3246 | 11월 꼭지글 (수정) [2] | 레몬 | 2012.11.10 | 2748 |
| 3245 | 11월 책 목차 | 레몬 | 2012.11.10 | 2833 |
| 3244 | 11월 오프수업 - 목차, 서문, 꼭지글 [2] | 콩두 | 2012.11.10 | 3371 |
| 3243 | 서문과 꼭지글 | 샐리올리브 | 2012.11.10 | 2682 |
| 3242 | 마흔과 오십의 경계에서 중년여성이 일어야 할 책 -서문과 꼭지글 |  | 2012.11.10 | 4781 |
| 3241 | 11월 과제 서문 과 꼭지글 | 학이시습 | 2012.11.10 | 2792 |
| 3240 | 11월과제 서문과 꼭지글 | 서연 | 2012.11.09 | 2732 |
| 3239 |
11월 오프 수업 과제 서문과 대표 꼭지글 | 세린 | 2012.11.09 | 7160 |
| 3238 | 11월 OFF 수업 과제 (서문, 꼭지글 포함) | 장재용 | 2012.11.09 | 2646 |
| 3237 | 꿈쟁이 뿌꼬 - 꼭지글 [1] | 한젤리타 | 2012.11.08 | 2934 |
| 3236 | 꿈쟁이 뿌꼬 - 서문 [2] | 한젤리타 | 2012.11.07 | 3038 |
| 3235 | 사람이 날아다니고 물이 거꾸로 흐르는 곳 [3] | 콩두 | 2012.11.05 | 4229 |
| » |
쌍둥이는 합동일까? 닮음일까? | 세린 | 2012.11.05 | 4415 |
| 3233 | 나의 오지 (prologue) [3] [1] | 장재용 | 2012.11.05 | 2633 |