- 세린
- 조회 수 12134
- 댓글 수 8
- 추천 수 0
논리적 스캔들, 루트2
- 피타고라스 학파가 숨긴 수
수직선을 그려보자. 우리는 먼저 직선을 그린다. 그리고 가운데 쯤 0을 표시한다. 0을 기준으로 오른쪽으로 적당한 간격을 유지하며 1,2,3,4 를 적는다. 왼쪽에도 마찬가지로 -1, -2, -3, -4 를 적는다. 직선을 길게 그린 친구는 좀 더 많은 숫자를 표시하겠지? 숫자를 몇까지 적느냐는 자유다. 그럼 이제 0과 1사이를 채워보자. 0과 1의 중점 2분의 1을 표시한다. 또 0과 2분의 1의 중점인 4분의 1 표시할 수 있다. 마찬가지로 2분의 1과 1의 중점 4분의 3도 표시할 수 있다. 이렇게 하다보면 0과 1사이가 숫자로 메워진다. 유리수, 즉 분수는 무수히 많기 때문에 우리가 다 표시할 수 없지만 사이사이를 채우다보면 촘촘하게 자연수와 자연수 사이, 0과 1사이, 0과 -1사이, 음수와 음수 사이가 메워질 것 같다. 피타고라스 학파도 그렇게 믿었다. 직선 위의 모든 점이 유리수로 덮혀질 수 있을 것이라고 생각하였다.
피타고라스는 탈레스 이후의 가장 뛰어난 그리스 수학자라고 어떤 책(<에우데무스 요약/ 프로클로스 지음>에 기록되어 있다. 하지만 피타고라스를 존경하고, 따르던 사람들이 그를 신비주의로 감쌌기 때문에 확실하게 알려진 것은 별로 없다. 피타고라스는 학교를 세웠는데, 이 학교는 철학, 수학, 자연과학을 공부하는 학파로서 비밀을 지키고 어떤 의식을 행하는 매우 단단하게 결속된 단체로 발전하게 됐다. 피타고라스 학파는 ‘정수가 만물의 근원’이라는 철학 위에 세워졌다. 이것이 수의 성질에 대한 찬미와 연구를 하게 했고, 기하학, 음악, 천문학과 더불어 산술을 기초 학문으로 했다. 그러던 어느 날, 피타고라스 학파는 공부하던 중, 수직선 위에 자신들이 알고 있는 유리수에 대응하지 않는 점의 존재를 발견했다. 한 변의 길이가 1인 정사각형의 대각선을 수직선에 표시하려고 보니 그 점과 대응하는 어떤 유리수도 없음을 깨달았다.
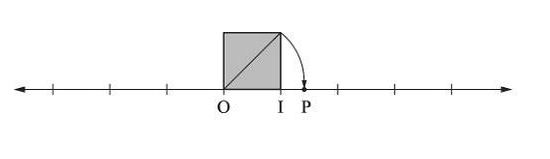
(그림1 : 점P에 해당하는 유리수가 없었다.)
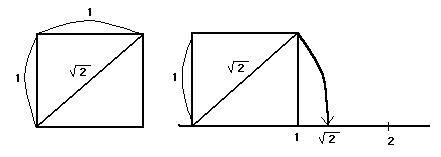
(그림2 : 점P는 바로 루트2였다.)
그들에게 그 사실은 아주 큰 충격이었다. 유리수가 아닌 수가 발견되다니, 피타고라스 학파는 혼란에 빠졌다. 무엇보다도 '모든 것이 정수에 따른다'는 피타고라스 학파의 철학에 치명적인 타격을 주는 발견이었다. 또 직관적으로 모든 크기가 어떤 유리수에 의해 표현될 수 있다고 믿었기 때문에 그것은 그들이 그동안 생각해왔던 것에 위배되는 것으로 보였다. 새로운 수의 발견은 도형을 다루는 학문인 기하학에도 충격을 줬다. 이것은 너무도 대단한 ‘논리적 스캔들’이었으므로 피타고라스 학파는 얼마 동안 이 문제를 비밀로 감추려고 애썼다. 전해 내려오는 이야기에 따르면 피타고라스 학파의 히파수스(Hippasus, 혹은 다른사람)가 그 비밀을 외부인에게 누설시켰다는 이유로 바닷속으로 내던져졌다는 얘기도 있다. 그들은 발견한 수에 이름을 붙여줘야 했다. 한 변의 길이가 1인 정사각형의 대각선은 루트2이고, 그들은 그것을 무리수라고 불렀다. 한동안 루트2가 사람들에게 알려진 유일한 무리수였다.
제곱근은 이렇게 사람들에게 발견됐다. 갑자기 왠 제곱근이냐고? 루트는 제곱근의 영어 이름이다. 제곱근2가 루트2다. 제곱근은 제곱의 뿌리, 뿌리는 영어로 하면 root, root의 r을 기호화 해서 루트 기호가 생겼다. ![]()
나무를 하나 상상해보자. 어떤 나무가 떠오르나? 나는 사과나무를 떠올렸다. 나는 2012년 10월에 문경새재에 가서 사과나무를 봤다. 실제로 보니 사과나무는 내가 어린시절 그렸던 것처럼 갈색 나무에 초록색 잎이 무성한 가운데 빨간 사과가 열려 있진 않았다. 어떻게 생겼든 사과가 주렁주렁 열린 나무를 상상해보자. 그리고 사과에 숫자를 붙여주자. 1부터 10까지 열개 만 선택해서 붙인다. 나무는 열매를 맺기 위해 영양분을 공급 받아야 한다. 지금 우리가 상상한 사과나무는 제곱이라는 영양분을 공급받으면 열매가 열린다. 그런데 1은 1의 뿌리에 영양분을 받고, 2는 2의 뿌리에, 3은 3의 뿌리이다. 10까지 마찬가지다. 열매 1부터 가지를 따라 뿌리까지 내려가보자. 어떤 수에 제곱이라는 영양분을 주면 1이라는 열매가 열릴까? 그렇다 1이다. 1을 제곱하면 1이된다. 그런데 우리는 음수도 알고 있다. 음수를 제곱하면 양수가 된다는 사실도 안다. 그렇다. 1이라는 열매는 -1이라는 뿌리를 제곱해도 1이 된다. 즉 1의 제곱근은 +1, -1이다. 이 둘을 합쳐서 플러스, 마이너스 1이라고 말해도 된다. 이번엔 열매 4번의 뿌리를 찾아가보자. 열매2와 3은 조금 이따 하자. 4는 어떤 수를 제곱하면 4가 될까? 2와 -2이다. 그렇다면 이번엔 열매 9를 해보자. 맞다. 3과 -3이 9의 제곱근이 될 것이다. 아직 안한 열매는 몇 번인가? 2,3,5,6,7,8,10이다. 열매 2를 맺으려면 어떤 뿌리에 제곱이라는 영양을 줄 수 있을까? 우리가 알고 있는 수 자연수, 음수, 유리수 중 아무리 생각해봐도 없다. 예를 들어, 1과 2사이에 있는 1.5를 제곱해보자. 그럼 우린 2.25를 얻는다. 그럼 1.5보다 0.1 작은 1.4를 제곱해보자. 그럼 우린 1.96을 얻는다. 그럼 1.41을 제곱해보자. 1.9881이다. 1.42의 제곱은? 2.0164이다. 계속해서 제곱해서 2가 되는 수를 찾아가다보면 끝이 안보인다는 사실을 깨닫게 된다.
피타고라스 학파는 피타고라스 정리를 알고 있었다. 직각삼각형에서 빗변의 제곱은 나머지 두 변의 제곱의 합과 같다. 즉 한 변의 길이가 1인 정사각형을 대각선으로 자르면 직각이등변삼각형 두 개가 생긴다. 이때 대각선의 제곱은 나머지 두 변의 제곱의 합인 2가 됐다. 그들은 제곱해서 2가 되는 수를 유리수에서 찾을 수가 없었던 것이다. 그들에게 루트2의 출현이 충격일 수밖에 없었던 이유는 ‘정수’에 대한 맹신이 있었기 때문이다. 자신들이 알고 있는 유리수가 수의 전체라고 굳게 믿고 있었는데, 그것이 아니라고 루트2가 등장했으니 얼마나 놀랠 일인가? 극단적으로 내 부모가 내 진짜 부모인줄 알고 있다가 어느날 갑자기 진짜 부모는 따로 있다는 이야기를 들었을 때의 충격과 같을지도 모른다.
제곱해서 2가 되는 수는 루트2와 마이너스 루트2이다. 열매 3번도 마찬가지다. 플러스, 마이너스 루트 3이 3의 제곱근이다. 5,6,7,8,10도 다 마찬가지이다. 제곱근이 정수인 것은 1,4, 9, 16, 25 등이다. 정수를 제곱해보면 쉽게 알 수 있다. 그러므로 1,4,9,16,25 등 이 사이에 있는 수들의 제곱근은 그 수에 루트를 붙여주면 된다.
제곱과 제곱근은 세트다. 제곱근을 제곱하면 정수가 된다. 정수의 제곱근은 대부분 루트를 씌우면 된다. 제곱과 제곱근 변화가 자유로운 친구들은 계산할 때 더 쉬워질 거다.
소크라테스가 그를 찾아온 학생에게 질문을 한다.
“여보게, 넓이가 1인 정사각형의 한 변의 길이가 얼마인가?”
학생이 대답한다.
“한 변의 길이는 1입니다.”
소크라테스가 다시 묻는다.
“그렇다면, 한 변의 길이가 1인 정사각형의 넓이의 2배가 되는 정사각형의 한 변의 길이는 얼마인가?”
학생이 자신있는 목소리로 대답을 한다.
“2이지요.”
한 변의 길이가 2인 정사각형의 넓이는 얼마인가? 여러분이 대답해보자. 2의 제곱은 4. 즉 넒이는 4이다. 그런데 소크라테스의 질문을 잘 살펴보면 넓이가 1인 정사각형의 2배의 넓이를 갖는 정사각형의 한 변을 구해달라고 했다. 즉 “넓이가 2인 정사각형의 한 변의 길이는?” 이란 문제를 낸 것이다. 우리가 답해주자. 한 변의 길이는 얼마인가? 루트2이다. (이쯤이면 제곱근이 무엇인지 감을 잡은 학생이 마이너스 루트2를 생각할 수도 있다. 하지만 지금 소크라테스의 질문은 도형이고, 길이는 마이너스가 없다는 사실을 캐취해야 한다.) 넓이가 3인 정사각형의 한 변의 길이는 루트3이다. 숫자를 더 크게 해보자. 넓이가 121인 정사각형의 한 변의 길이는? 루트121. 맞다. 그런데 11이 더 정확하게 이야기 한 친구다. 121은 11또는 -11을 제곱하면 된다. 그러니 루트121은 11과 같은 숫자이다. 평소에 제곱 계산을 많이 해본 친구는 제곱근도 빨리 캐취할 수 있을거다.
개념 이해가 안 된 친구는 이 글을 다시 천천히 읽어보면서 중간중간 등장하는 문제를 풀어보자. 개념 이해가 됐지만, 121의 제곱근이 금방 떠오르지 않는 친구들은 먼저 1부터 숫자를 늘려가면 제곱 연습을 해보면 좋다. 개념 이해도 됐고, 121의 제곱근도 금방 이야기 할 수 있는 친구라면 무리수의 성질 및 사칙계산 연습을 더하면 좋겠다.
<참고>

(그림 3 : 피타고라스 ( 기원전 580년 경 - 기원전 490년 경))

(그림 4: 표도르 브로니코프(Fyodor Bronnikov)가 그린 <일출을 축하하는 피타고라스 학파>)
| 번호 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|
| 3352 | 핸드폰으로 3분 영상 일기 쓰기 [4] | 샐리올리브 | 2013.01.28 | 3397 |
| 3351 | 관리된 욕망 [1] | 파에톤 | 2013.01.28 | 2816 |
| 3350 | 직원이 중심이된 회사, 고객이 중심이 된 회사. [2] | 학이시습 | 2013.01.28 | 2770 |
| 3349 | 너는 몇 세기에 살고 있니? [4] | 세린 | 2013.01.28 | 3000 |
| 3348 | 알려지지 않은 신 11 [1] | 레몬 | 2013.01.28 | 2387 |
| 3347 | 뿌꼬(2)_잠실역 4-3 [2] | 한젤리타 | 2013.01.28 | 2724 |
| 3346 | 나에게 신화란 무엇인가? [2] [2] | 콩두 | 2013.01.21 | 3046 |
| 3345 | #1 그냥쓰기_백사마을 [3] [1] | 서연 | 2013.01.21 | 3406 |
| 3344 | 난 어떤 부류의 사람인가 [1] |  | 2013.01.21 | 7919 |
| 3343 | 파에톤, 그 화끈한 한판 [2] | 파에톤 | 2013.01.21 | 3522 |
| 3342 |
랑랑을 통해 배우는 청중과의 교감 | 샐리올리브 | 2013.01.21 | 3024 |
| 3341 | 뿌꼬 [5] | 한젤리타 | 2013.01.21 | 3231 |
| 3340 | 소설가의 탄생 [6] | 레몬 | 2013.01.21 | 2389 |
| 3339 | 위대한 기업 다 어디로 갔을까? [4] | 학이시습 | 2013.01.20 | 2527 |
| » |
논리적 스캔들, 루트2 | 세린 | 2013.01.20 | 12134 |
| 3337 | 발표 자료 [3] | 파에톤 | 2013.01.15 | 2471 |
| 3336 |
발표 자료 | 레몬 | 2013.01.15 | 2824 |
| 3335 |
신화야~~~~ 놀자! 놀자!^^ | 콩두 | 2013.01.15 | 2789 |
| 3334 |
1월 오프 수업 정리 _수학하는 세린 | 세린 | 2013.01.15 | 4224 |
| 3333 | 욕망은 이해할 수도 설명할 수도 없는 그 무엇 [1] |  | 2013.01.15 | 5445 |